Hoy volvemos a tratar el tema del trazado de una rueda, si bien en este caso es la de diez, que aunque no es tan abundante como la rueda de ocho, posee una serie de propiedades que la hacen especialmente singular y elegante, y por ello la elegí como logotipo de este blog. En primer lugar, su trazado surge de una manera menos sencilla e inmediata que el de ocho, pero al tener dos brazos más, las proporciones tanto de los sinos como de los azafates, resultan más armónicas, debido a que los vértices situados sobre los ejes son agudos, confiriendo un aspecto más estilizado a ambas figuras.
Sin embargo, la característica que de verdad hace que el trazado de «diez lefe» sea considerado como el más perfecto de todos, es que puede componerse única y exclusivamente con ruedas de diez, sin necesitar para nada ruedas de otro número diferente de brazos, a las que se denomina desculatadas. Por si fuera poco, los candilejos, que son unas pequeñas estrellas de cinco puntas que aparecen junto las aspillas de cualquier rueda, poseen una forma perfectamente regular, y es en el único trazado en el que aparecen así. Un ejemplo extraordinario de trazado diez lefe lo podemos encontrar en la iglesia del monasterio de San Antonio el Real (Segovia).

Tal y como ya se hizo con el ejemplo de ocho, procederemos a diseñar nuestra rueda de diez a calle y cuerda, es decir, con una distancia entre brazos (calle) igual al doble de la anchura de un brazo (cuerda). En su día os comentaré por qué la calle y cuerda era tan popular en el oficio, ya que se debía a un tema puramente práctico a la hora de trabajar con las maderas en el taller. Huelga decir que los métodos de trazado que propongo están pensados para que cualquiera pueda realizarlos con escuadra, cartabón y compás, ya que si lo que se usa es un ordenador, sale mucho más rápido mediante una serie determinada de comandos.
El primer paso consite en dibujar dos ejes perpendiculares y un círculo con centro en el cruce de ambos, con un diámetro a elegir, aunque se consigue mayor precisión cuanto mayor sea.
Con el mismo radio que acabamos de usar, y con centro en A, trazamos un arco que pase por el centro de la 1ª circunferencia (punto B). Las interseciones con dicha circunferencia serán los puntos C y D. Unimos los puntos C y D con un segmento y en la intersección con el diámetro AB señalaremos el punto E.
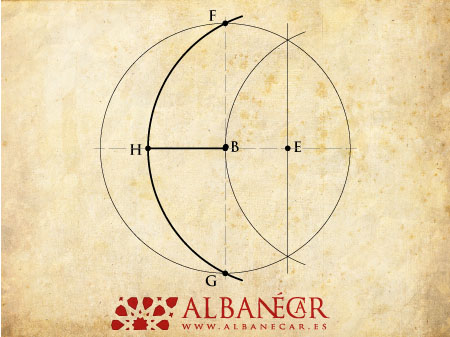
Con centro en E, y radio EF ó EG (los punto F y G son simplemente intersecciones del diámetro vertical con la primera circunferencia), trazamos un arco. El punto de intersección de dicho arco con el diámetro horizontal será denominado H, y la distancia BH será la cuerda de arco que nos permitirá dividir la circunferencia en 10 partes iguales.
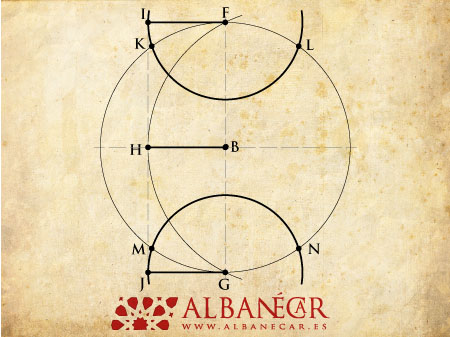
Ahora procedemos a trazar dos arcos, con centros en F y G, y con un radio igual a BH. De esta manera, uno tendrá centro en F y radio FI, y otro tendrá centro en G y radio GJ. En el primer arco, las intersecciones con la 1ª circunferencia serán los puntos K y L, y en la segunda, M y N.
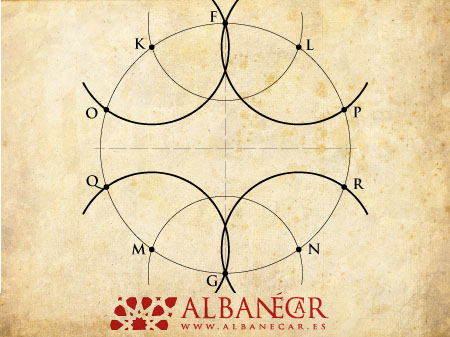
Nuevamente con el mismo radio usado anteriormente, trazaremos otros 4 arcos. Con centro en K y radio KF obtendremos O; con centro en L y radio LF obtendremos P; con centro en M y radio MG obtendremos Q, y con centro en N y radio NG obtendremos R. Si quisiéramos comprobar la exactitud de la división en 10 partes, al usar el mismo radio con centro en cualquiera de los puntos marcados en la circunferencia, un arco debería pasar exactamente por los dos puntos adyacentes.
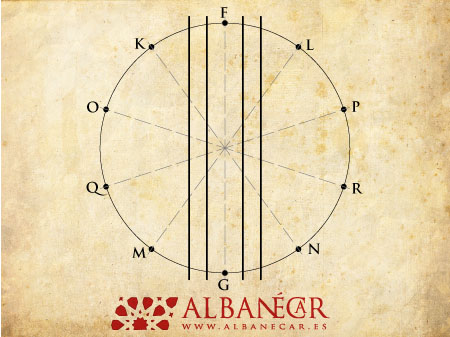
Pasando por el centro de la circunferencia inicial, podemos trazar los 5 diámetros que marcarán los ejes de la rueda (FG, LM, PQ, RO, y NK). Tras ello, por fin podremos dibujar cuatro líneas paralelas a uno de los ejes, dos a un lado y dos a otro, conservando entre ellas la distancia equivalente a una cuerda. A partir de ahora el procedimiento va a ser semejante al que ya realizamos con la rueda de ocho.
Se repite el mismo procedimiento una vez por cada eje restante. Tendrás que ser muy minucioso a la hora de trazar las paralelas, ya que la mínima desviación hará que la estrella de 10 no tenga todos sus vértices iguales.
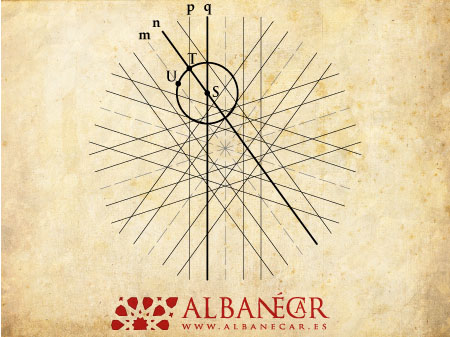
Ahora, seleccionaremos un eje y un segmento paralelos, y dos segmentos de la dirección más próxima, de manera semejante a la del dibujo y los denominaremos m,n, p y q. Presta atención a que m es un eje y no un segmento. En la intersección de n con q, marcaremos el punto S. En la intersección de n con p marcaremos el punto T. Con centro en S y radio ST, dibujaremos una circunferencia, cuya intersección con m nos dará el punto U.
Con centro en U y usando el mismo radio, en este caso US, trazamos otra circunferencia, y donde interseque con m, señalaremos el punto 1. Con centro en B (el centro de la 1ª circunferencia que se trazó) y radio B1, se dibuja una nueva circunferencia, cuyas intersecciones con los ejes principales serán los puntos 1,2,3,4,5,6,7,8,9 y 10. Date cuenta de que esta circunferencia no tiene nada que ver con la primera, que únicamente se usó para dibujar los ejes. Ahora los nuevos puntos servirán para dibujar la rueda en sí.
Une los puntos consecutivos con líneas que los sobrepasen ampliamente, a la manera del dibujo, y luego traza una paralela por el exterior que diste una cuerda de la anterior.
Ahora comienza a dibujar la rueda, remarcando las figuras principales. En el centro está el sino, rodeándolo están las almendrillas y azafates y en el exterior las aspillas.
Una vez dibujados los contornos de las figuras, empieza a tener en cuenta el entrelazado, donde una misma cinta tiene que estar pasando por encima o por debajo alternativamente, sin excepción. Hay quien lo llama el «corta y pasa». Da igual por donde comiences, una vez establecido el primer lazo, los demás salen automáticamente. Dependiendo de la finalidad de tu rueda, puedes rematarla como en el dibujo, o incluirla en un trazado más amplio.
Y finalmente, si lo que quieres es representar una rueda de carpintería tradicional, le puedes añadir el agramilado, siempre respetando el orden del lazo y el emboquillado.
Y esto ha sido todo. Aunque la explicación es larga, el resultado merece la pena, pues la rueda de diez es una figura fascinante cuyas propiedades geométricas nunca dejan de sorprender. En otro post explicaré el trazado diez lefe, que se genera mediante una trama de ruedas de diez y que está considerado el más perfecto de toda la lacería.










Manifica explicacion de trazado de rueda de diez, visito por primera vez este sitio y sorprende el carácter didáctico de las exposiciones de los diferentes temas, soy carpintero y he tenido la suerte de hacer alguna cubierta de madera, utilizare estos consejos en adelante. Felicidades por este magnifico sitio gracias y a continuar.
Hola Benjamín, muchas gracias por tu comentario, y me alegro de que el blog te sea útil. Respecto a la rueda de diez, puede que algún día dibuje otro método más preciso, porque a la hora de trazar las paralelas, si no se hace con cuidado se desvirtúa mucho el trazado. Un saludo.
Tengo una duda, «cuerda»es el grueso de la madera? El espacio entre las dos maderas?O el conjunto, espacio central y dos maderas, y otra mas, las escuadrias comerciales en la actualidad no tienen correspondencia con las que se utilizaban, se podria hacer con maderas de por ejemplo 10×7,5 de grueso?, gracias de nuevo.
Hola Benjamín, en efecto, la cuerda es el grueso de las maderas, mientras que el espacio que queda entre dos maderas es la calle. Y un trazado «a calle y cuerda» es aquel en el que la calle es igual a dos cuerdas. Por supuesto, hoy en día las escuadrías no tienen nada que ver con las antiguas. Una muy habitual para los pares era la de «octava y doceava», que se podría aproximar mucho con maderas de 10 de alto por 7 de grueso. De nada, un saludo y hasta pronto!
Conozco un método curioso para trazar decágonos mediante una cuadrícula. salen perfectos. llevo años investigando estas cosas por mi cuenta hasta que encontré el libro carpintería de lo blanco de lopez de Arenas. y buscando un dato ha aparecido tu blog. ¡¡enhorabuena!! es fantástico. siempre me llamaron la atención las lacerias y los atauriques. ¿cómo hacer para contactar contigo? saludos y gracias
Hola Antonio, aunque ya te he respondido por el correo, tampoco quería dejar de hacerlo por aquí. Me puedes escribir al email: correo [@] albanecar . es
Un saludo!
Saludos de nuevo, quiero consultar un detalle en limas dobles o limas mohamares, solo estan en contacto las cabezas de los pares con los cortes acoplados? , y otra duda, los pares son igual de altos que las limas? Y pasan a media madera en su encuentro con las limas?. Muchas gracias.
Hola Benjamín. Buenas preguntas, sí señor. Te las puedo contestar, pero me temo que sin dibujos va a ser un poco complicado hacerme entender, aunque habrá que intentarlo. Antes que nada, para que hablemos con propiedad, los pares que acometen a las limas se llaman péndolas. En general las péndolas muestran un corte liso en la cara que va unida a la lima, y la unión se resuelve mediante uno o dos clavos. Nunca se hacían ensambles a media madera por un simple motivo: Debido a que cada faldón se montaba en el suelo y luego se izaba, a la hora de colocarlos en su sitio y dar los toques finales a la armadura, se producían ligeras imperfecciones, movimientos, etc., que era necesario corregir. Si las péndolas atravesaran la lima mediante un ensamble, cualquier error saltaría a la vista al unirse entre ellas y quedar desplazada una respecto a otra. Por ello, se utilizaban las arrocabas, que eran piezas que simulaban ser las prolongaciones de las péndolas, pero que eran independientes, de manera que se podían corregir los desajustes inclinándolas o desplazándolas respecto a su posición «ideal».
Por otra parte, en el caso de las limas mohamares, su alto es igual que el de los pares, al formar ambas piezas parte del mismo faldón, y cuyas caras anterior y posterior eran coplanares entre todos los elementos. No sucede lo mismo en las limas bordón, que no forman parte de los faldones ni poseen caras coplanares.
Un saludo.
Y una rueda de once?
Muchas gracias por esta aclaracion, en realidad una clase magistral, insisto en el lenguaje didáctico y funcion formadora de estas paginas,
en este dificilisimo campo de la construcción de armaduras de madera.Felicidades
Muchas gracias por vuestra página, Albanécar.
Como estudiante de Historia del Arte, vuestra página me ayuda a aclarar y a ampliar información sobre conceptos relativos a la carpintería lo blanco.
Saludos cordiales desde Valladolid.
Muchas gracias por haber creado esta página yo solo soy un estudiante de 5 de primaria y empecé a utilizar esta página debido a que un profesor nos mandó un proyecto a todo sobre ruedas de laceria. Gracias a esta página e podido llagar a entrelazar varias ruedas entre sí y a comprender mucho mejor las ruedas de laceria. Muchas gracias
Pero tengo una pregunta. Sería posible hacer una rueda de 12 por ejemplo?